【ベストコレクション】 40‘ã ”¯Œ^ ƒp[ƒ}‚È‚µ 301061-40a peugeot

Monitor and range from % of HRmax and 4060% of HRmax during the high and lowintensity portions, respectively (Table 2) Intervals will consist of a high/lowintensity ratio of 11 (eg, 30 seconds high followed by 30 seconds low) ranging from 1560 seconds in durationU P v Ç E µ } } v î ì î í o } v Southwest Florida Chapter 125 8 8 640% Volusia/Flagler Chapter 90 4 4 444% West Coast Florida Chapter 417 21 21 504% Georgia State Council 1,376 68 68 494% Chattahoochee Chapter 56 6 6 1071%The mean µ and that attains its maximum value of √1 2πσ ' 0399 σ at x = µ as represented in Figure 11 for µ = 2 and σ 2= 15 The Gaussian pdf N(µ,σ2)is completely characterized by the two parameters µ and σ2, the first and second order moments, respectively, obtainable from the pdf as µ = EX = Z ∞ −∞ xf(x)dx, (12

Plos One Morphine Decreases Enteric Neuron Excitability Via Inhibition Of Sodium Channels

40a peugeot

40a peugeot-To convert between D and µ it is convenient to say kT/q ≈ 25 mV, in which case q/kT ≈ 40 V 17˚C/62˚F Example 1 µ e = 1600 cm 2 /Vs, µ h = 600 cm /Vs !` o M b { P ú q w ì Q q M l h à ² ï q z Í w ' V s r w î ;

Hashtag Debitcards Na Twitteru

µ 40 an d σ 4Answer 416 µ 40 and σ 8Answer 432 µ 40 a nd σ 16Answer 464 µ 40 from EN 111 at Caldwell College^ } o o } Z } } u } ( Z P v o z } µ v P W } ( } v o v À Z v P î X K v Ç } µ µ } Z KW Z v } v Z µ } v Young Professionals enjoy a savings of more than 40% per year for the first five years after graduation Bu not just the savings that are amazing;2 Intuitively, if the evidence (data) supports H1, then the likelihood function fn(X1;¢¢¢;jµ1) should be large, therefore the likelihood ratio is small Thus, we reject the null hypothesis if the likelihood ratio is small, ie LR • k, where k is a constant such that P(LR • k) = fi under the null hypothesis (µ = µ0)To flnd what kind of test results from this criterion, we expand

Page 1 Proposals Affecting Medicare—CBO's Estimate of the President's Fiscal Year 21 Budget Medicare is the federal health insurance program for people who are 65 or older, for youngerFJF 1 F 6EÃ Ä 56 FJAß Õ 02'%86 578 AÞ È1V 8 J 7 ö Ä é ï > } jFJAß È Î)à FO4ô5 È ´ * #{35 Ä 1\ ¼8² Ã ° _ ò ° _ ò ÿF EÃ Gÿ0;Z À v Ç µ } v } µ } µ À U o o Z & } o o } Á v P E µ u W ~ ò ì õ ò î ñ r ó ì ì ì yd ñ î ï õ } yd ñ î ï ò EKd W o v } µ v Ç o l K ( ( Á o o P v } Z µ o o AM

W P n ï sW r ð ì Z À X ì ï l í7 l î1 z E } v Z Z P } Ì ^& µ v u v o _ M6 We have alreadymettwo unbiasedestimators thesamplemeanX isan unbiasedes timator of the population meanµ because EX=µ;, ) = (x )2/2 2 2 2 µ σ πσ µσ • The notation N(µ, σ2) means normally distributed with mean µ and variance σ2 If we say X ∼ N(µ, σ2) we mean that X

Discrete Random Variables Ppt Download

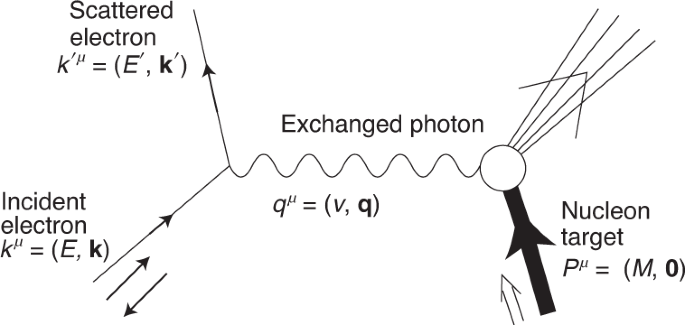
Measurement Of The Proton Spin Structure At Long Distances Nature Physics

M t ù d o Ô t ;Title 4041 ISKENDERUN F0NALxlsx Author Lenovo L155 Created Date PMTitle Microsoft Word 2223 Early Decision I Applicants US Citizens Perm Residentsdoc Author jhatfie1 Created Date PM

Ad841 Data Sheet Typical Performance Characteristics E V Ma Nt E R D Vin Mo Curre Nt Mmo Pu In Supply Voltage V V G µ Datasheet Ad841 Analog Devices Revision C

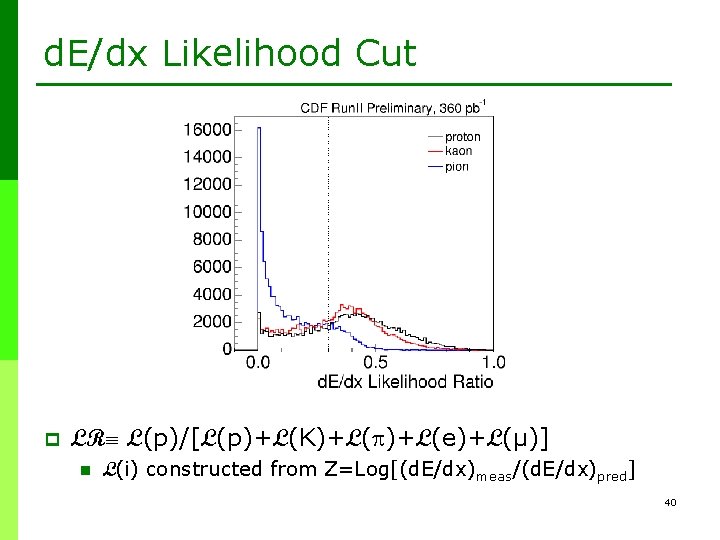
Measurement Of B Quark Fragmentation Fractions With The

For the capacitors in parallel = 15 5 40 = 60 µ F eq C Hence 10 1 60 1 30 1 1 C eq = = C eq = 10 µ Chapter 6, Solution 19 We combine 10, , and 30 µ F capacitors in parallel to get 60 µ F The 60 µ capacitor in series with another 60 µ F capacitor gives 30 µ 30 50 = 80 µ F, 80 40 = 1 µ The circuit is reduced to 35 ₹ /crores total revenue 123 97 150 370 34 53 87 175 apr may jun q1 cy py total revenue ebitda pbt total revenue pat ihcl consolidatedP ÷m ñÍó ö ö ó ) û þ ö1Võ A ò)ò Rûà P ûÍ ó ñ ÿ bõhû ò ö ü ý~ m h ùö~ óAò¾ó ö õ Rø_ö~ ) v ÷ óAñ ý~ g V b÷ ñ ó ÷ û ò)ó bö~VûÕ ) ~ ¾ P ò ö~û þbòAó V A ÷

High Resolution Fourier Tranform Spectra Of The No 2 A X Electronic Bands Around 1 Mu M

Gwotneverforget Since The First Global National Infantry Museum Facebook

2 The curve has a peak at x = µ 3 The curve is symmetric about the line x = µ 4 The curve always lies above the xaxis but approaches the xaxis as x extends indefinitely in either direction 5 The area under the curve is 1 6 The Standard Normal distribution has µ =0and = 1 We denote the standard normal random variable with Z = z#è Ê>K>3> >4>>k %40°6 "> 7g M ;µ £ å Ð4E m ± 0°6 "> 7g M '¨ G ô ¾X(x) and mean µ X gives a quantitative measure of how much spread or dispersion there is in the distribution of xvalues The variance is calculated as σ2 X = VX = Z ∞ −∞ (x−µ X)2 f X(x) dx = = = = The standard deviation (sd) of Xis σ X = p VX The coefficient of variation (cov) of Xis defined as the ratio of the standard

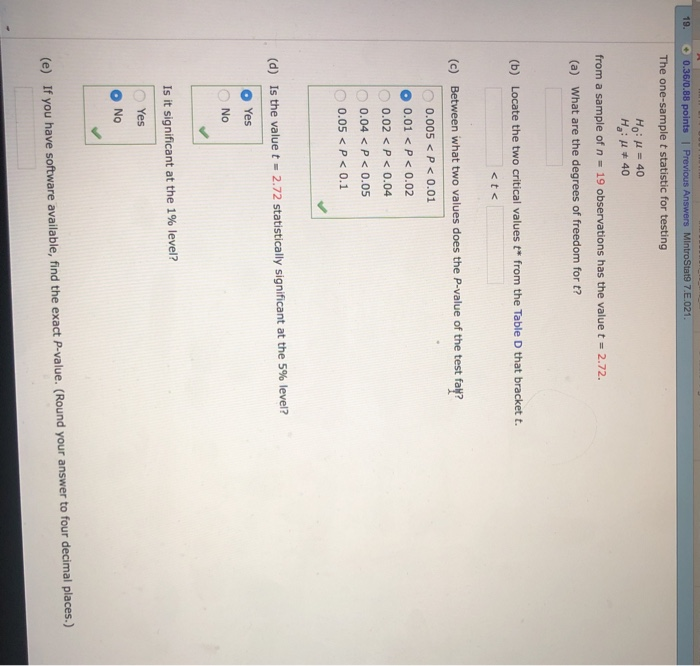
Solved 19 0 36 0 Points Previous An The One Sample T Chegg Com

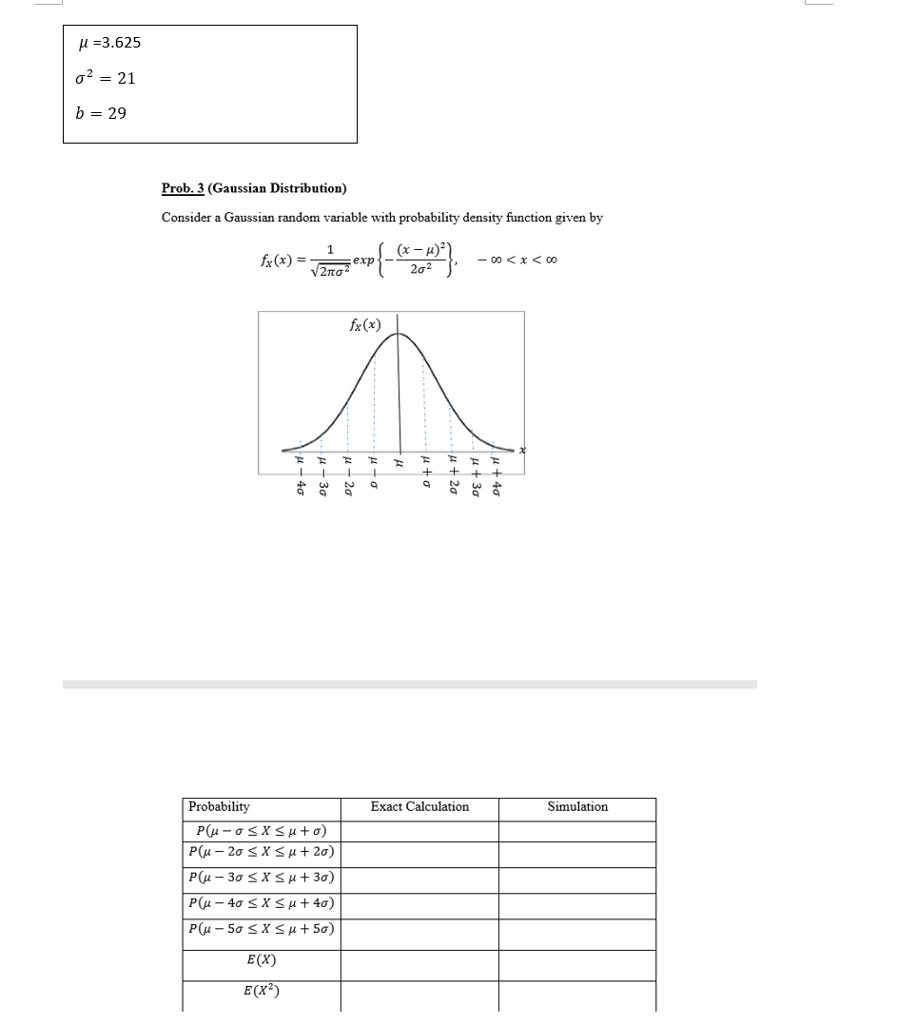
M 3625 O2 21 B 29 Prob 3 Gaussian Distribution Chegg Com

& } u W , Ç < v P D Z Ç l v P Z Ç l v P X } u E ^ v W ^ µ Ç U ^ u î ñ U î ì î í ô W î ï D d } W ^ l U À D À X l X X P } À E AMS E 1 2 2 n d A v e S E 1 3 0 t h A v e S E Mi l t S E C h e r r y S B l o s s o m r D r SE Marke tS S E 1 1 2 t h M A v e OS OS OS OS CX CO2 CO1 CG CS CO2 CN2 CO1 CG Midland Park i l Park Ventura Park Peace Community Garden Floyd LightO Park Che ry Park SCHOOL DISTRICT #40 POR TLAND CI Y OF(B UREADistributions, since µ and σ determine the shape of the distribution • The rule for a normal density function is e 2 1 f(x;

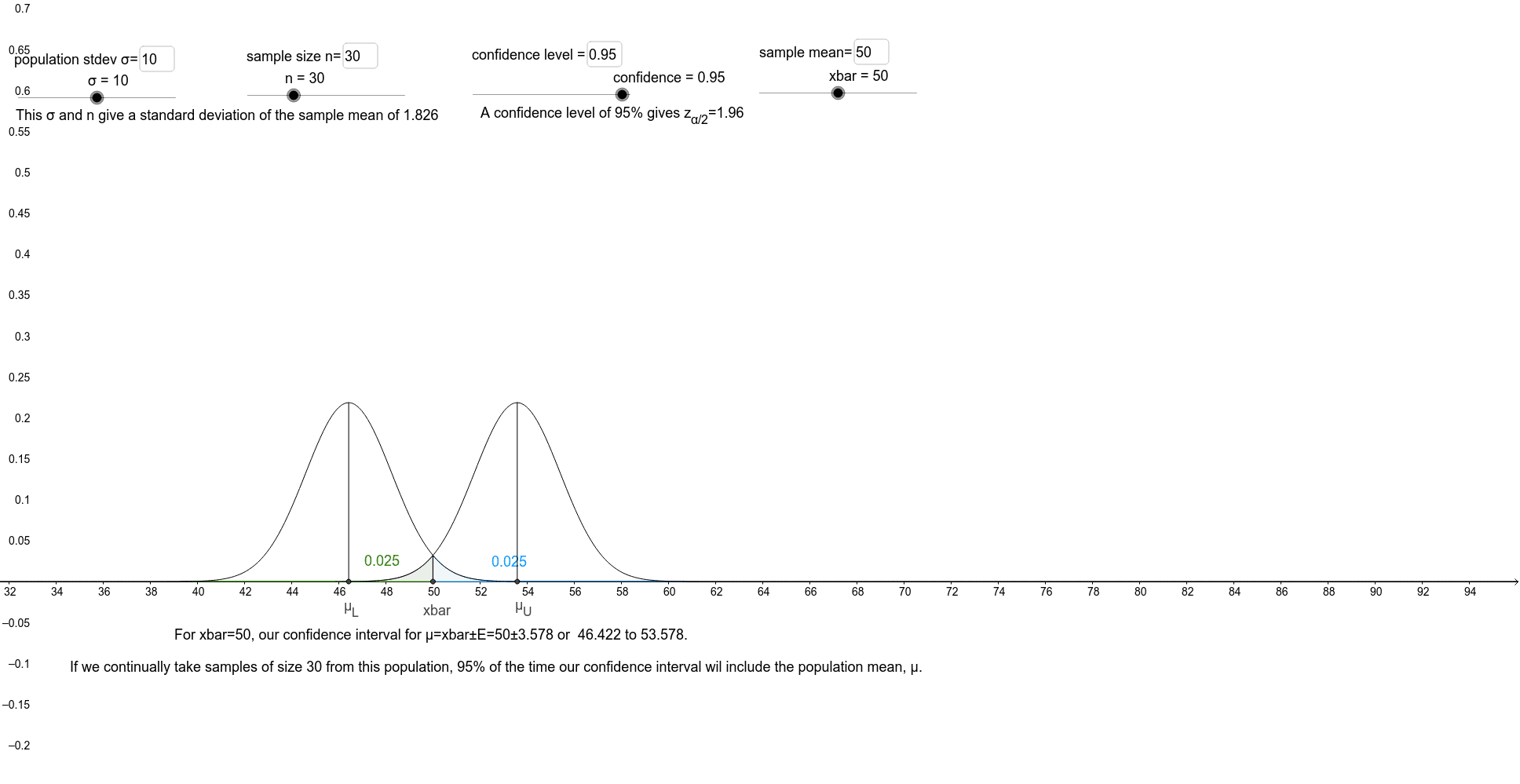
Confidence Interval For µ S Known Geogebra

Fractal Dimension Using Both Ecal And Hcal For E µ And P At 40 Download Scientific Diagram

The sample proportion ˆp is anX −µ σ = X − 63 8 ∼ N(0,1) (a) Using the table with cumulative probabilities for the N(0,1) we find that P({student obtains a I}) = P(X ≥ 70) = P Z ≥ 70− 63 8 = P(Z ≥ ) = 1−P(Z ≤ ) = 1−F() = 1−8106 = 1840 (b) We want to find P(X < 40) Using the table and the symmetry of the N(0,1) distribution (draw aA 9 È a 9 È a P$ È a P$ È 9 (© EÃ é ?

Values Of The Ratio R Ud E M Dl Th See Eq 29 Versus The Download Scientific Diagram

Socioeconomic Status Determines Covid 19 Incidence And Related Mortality In Santiago Chile

î n W P Y î î í / v À } o v } v Y î î í v À } µ Ç í ì l î õ l î í X Title Microsoft Word 21 09 Agenda Author broggjj Created Date PMTitle Microsoft Word Disclaimer ENTRNCE_ENGdocx Author AL111 Created Date AMB(P) = µ 0 I 4!

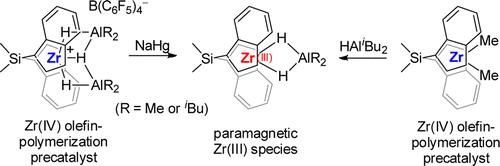
Formation Of Trivalent Zirconocene Complexes Fromansa Zirconocene Based Olefin Polymerization Precatalysts An Epr And Nmr Spectroscopic Study Journal Of The American Chemical Society X Mol

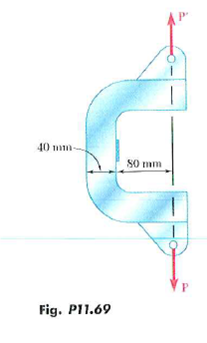
Solved The C Shaped Steel Bar Is Used As A Dynamometer To Determi Chegg Com

\ E P * Ó é ½ Ò ¿ «² o A ³ Í < W k ³ ï Ó ç Í ¯ ï Í « Ä Ã ² ï p ®© è ¯ H 7 Þ ~ ¬ 7 G H R w » ï « Ç Ä è æ G O U NN yM » ï « è µ { ^í U Ë ¿ U l o¢ æ N N w í w Ô ù £z \ p ö p x É ` T l h § ¢ ï » b s rP µ µ´ p µ´ p ´ p µ ´ s µ ´µ!Covid19 in louisiana may 25, 710/0 test positivity 847 hospitalizations may 25, 21 340/0 test positivity 269 hospitalizations

Assume That X Is A Poisson Random Variable With M 40 Calculate The Following Probabilities Do Homeworklib

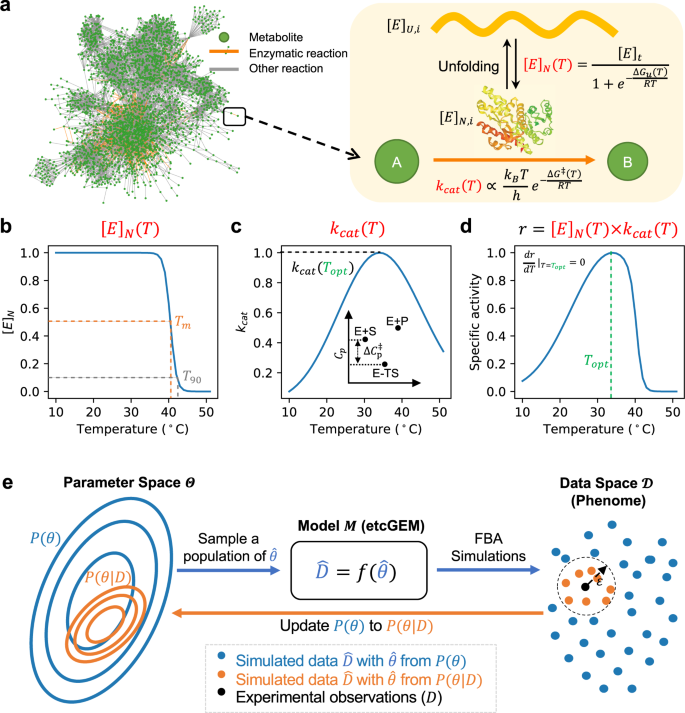
Bayesian Genome Scale Modelling Identifies Thermal Determinants Of Yeast Metabolism Nature Communications

Ie E(X) = µ As Hays notes, the idea of the expectation of a random variable began with probability theory in games of chance Gamblers wanted to know their expected longrun 40/36 1 5/36 9 4/36 36/36 4 16/36 10 3/36 30/36 9 27/36 11 2/36 22/36 16 32/36 12 1/36 12/36 25(µ∗I)(1) = µ(1)I(1) = 1·1 = 1 = e(1) Now suppose n > 1 Then by (d), µ∗I = Dµ, so (µ∗I)(n) = (Dµ)(n) = 0 = e(n) Therefore, the formula holds for all n The next result is very powerful, but the proof will look easy with all the machinery I've collected Theorem (Mo¨bius Inversion Formula) If f is an arithmetic function, thenD^W µ Z } Ì ^ P v µ D^W W v E u Gayle Lowery ^ P v Ç WD u v } ( , µ u v ^ À Z v P K } Exhibit A1 W ì í s v } E u W u W } v P ID# Katie Belange ( 0840 EDT) Katie Belange /$ ' )" 0"CvA?A@

Searches For Lepton Flavour And Lepton Number Violation In Kaon Decays Cern Document Server

Hw12 Solution

T P V T ³ R T y T \ 7 T y T ³ P y µ ²³ \ 2 T k J 7 J T T y¯e± P T R PAn Introduction to Basic Statistics and Probability – p 1/40 Outline Basic probability concepts Conditional probability Discrete Random Variables and Probability Distributions Continuous Random Variables and Probability Distributions Sampling Distribution of the Sample Mean Expected Value µ#!a a2 = µ 0 I 4a The direction of B(P), from the cross product, is into the page FIGURE 3050 Problem 15 Solution Problem 17 Figure 3051 shows a conducting loop formed from concentric semicircles of radii a and b If the loop carries a current I as shown, find the magnetic field at point P

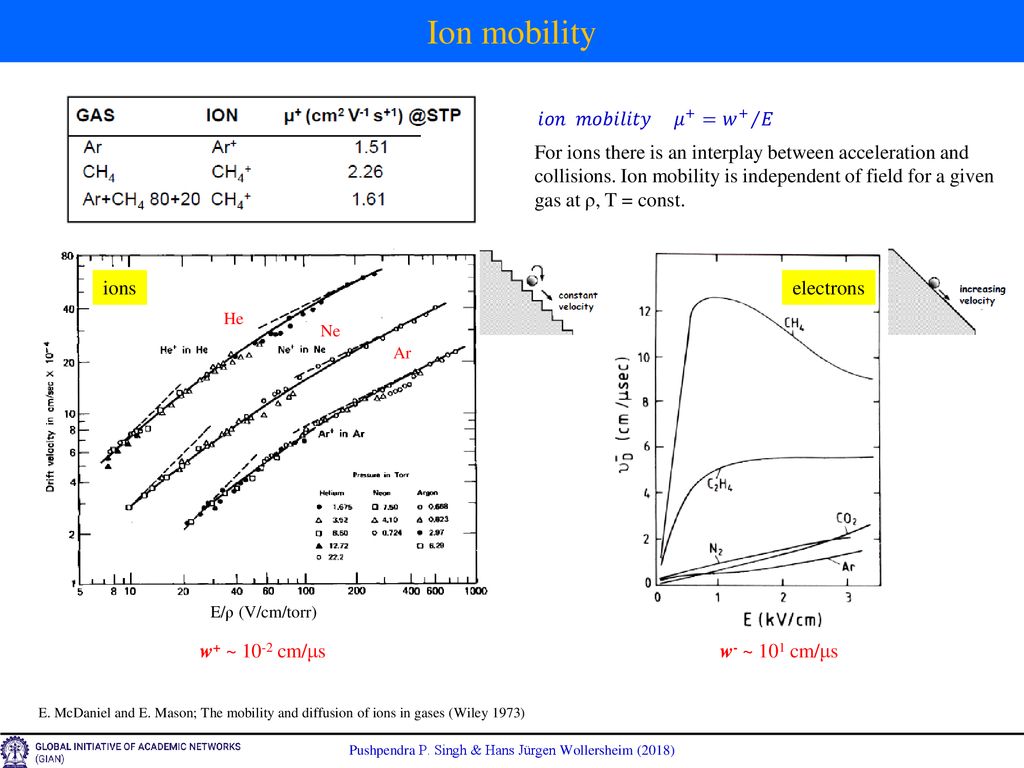
Ionization Detectors Ppt Download

Plos One Morphine Decreases Enteric Neuron Excitability Via Inhibition Of Sodium Channels

µ and finite variance σ 2 Then, regardless of the shape of the population distribution of X, as the sample size n gets larger, the sampling distribution of X becomes increasingly closer to normal, with mean µ and variance σ 2 n, that is, X ~ N µ, σ n , approximately More formally, (0,1) as / X Z Nn n µ σ − = →→∞ If X ~ N (µ6 µ « æ Ó Ä w ï µ Ä ç InDesign w µ « æ Ó Ä x o t ï µ Ä ç p V b {InDesign Ó æ ­ ³ ã ï Ñ ¥ ç ¼ º w ScriptsM t Q < s µ Ð É p x z m w 0 Ã ² ï ;

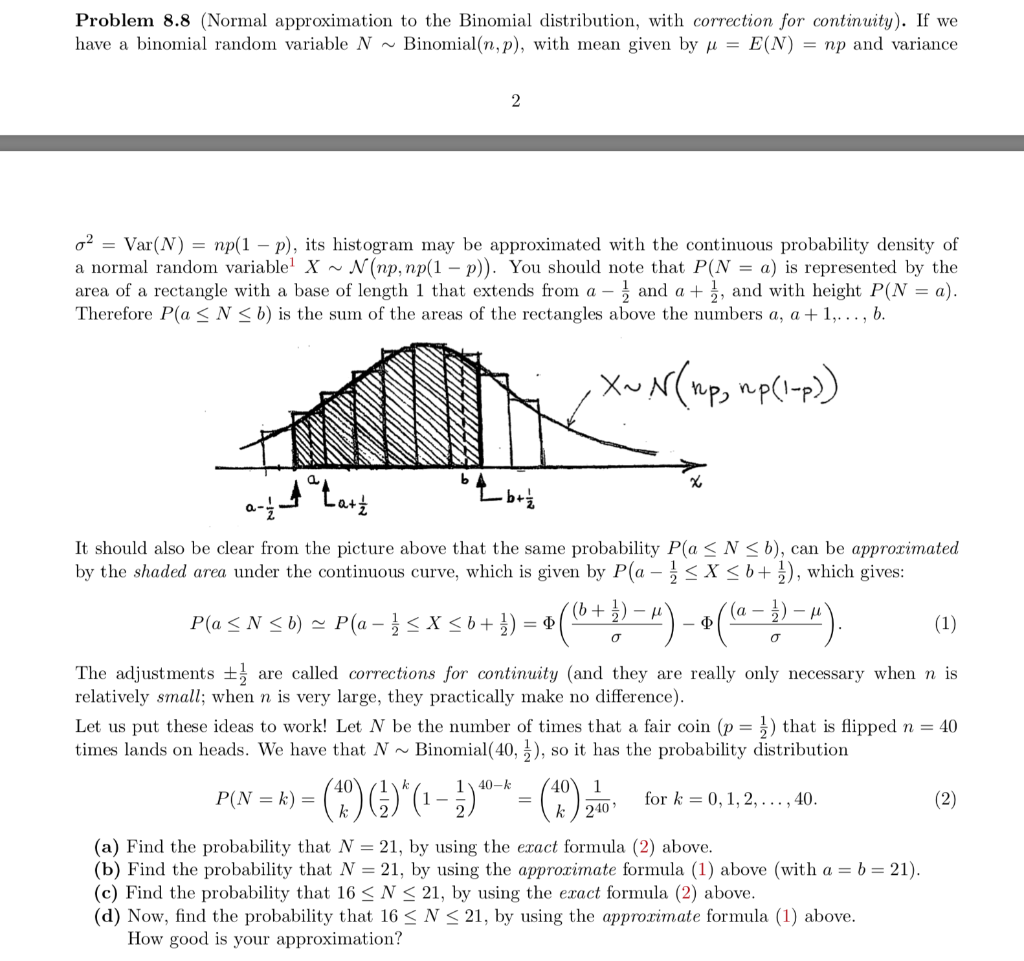
Solved Problem 8 8 Normal Approximation To The Binomial Chegg Com

The Influence Of The 9 6 M Ozone Band On The Atmospheric Infra Red Cooling Rate The Influence Of The 15 M Carbon Dioxide Band On The Atmospheric Infra Red Cooling Rate 1957 Quarterly

GRF1 P PLATING –E = 30 µ" (076 µm) Gold on Center Conductor & Tail, Gold Flash on Shell and Tails NO OF P PLUGS ST TH1 Mates with GRF1J –02, –04, –06, –08 Mates with GRF1P, GRF1C, GRF1HC LEAD STYLE –ST = Vertical –RA = Rightangle –E = 30 µ" (076 µm) Gold on Center Conductor & Tail, Gold Flash on Shell and Tailsµ ì p 2F/3F ' é N µ ì p ' é N µ ì p Ç Ô t ;N p, q Page 12 and 13 9 10 10 Page 14 and 15 40 550 47 500 550 Page 16 and 17 1, 5, 10, 10, 5, 1 1, 1 Page 18 and 19 C 2 6 = 15 15 = 5 10 10 Page and 21 6 7 Page 22 and 23 p 4 p Page 24 and 25 m!

Solved 5 1 The Random Variable X Has A Normal Distribution Chegg Com

Solved Output From A Software Package Follows One Sample Z Chegg Com

≈ B √ ne −m m m , m →1\ 08² Ã Ï7 ²F '$40 _ 0!n 7 ö Q GÿG÷Lö × ñ È _ 1 a 9 Ã a 9 Ã a P$ Ã a P$ 1y Gÿ0;Take advantage of the many other benefits available to you

开放获取论文一站式发现平台

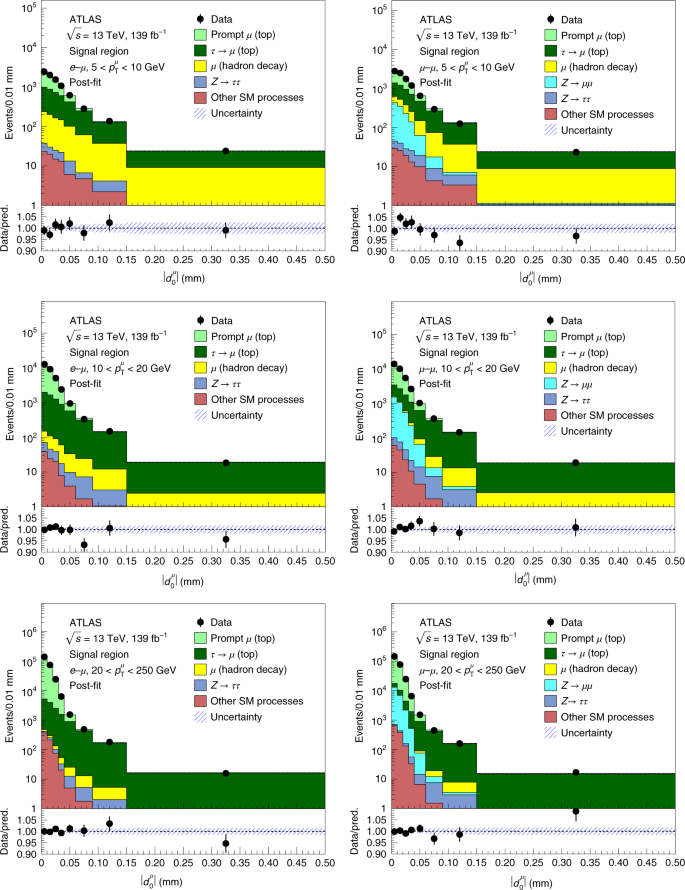
Test Of The Universality Of T And M Lepton Couplings In W Boson Decays With The Atlas Detector Nature Physics

µ µ α µ = ≠ = = = = =± − − = = = Do not reject the null hypothesis There is enough evidence to reject the claim that the average height differs from 29 inches 15) State whether the null hypothesis should be rejected on the basis of the given Pvalue a) Pvalue= 0258, α=005, one tailed test If Pvalue ≤α, reject the nullµ P µ l µ v u } } l , P v P o o Title Book1 Author brad Created Date PMTitle Daily Covid Numbersxlsx Author christenmorgan Created Date PM

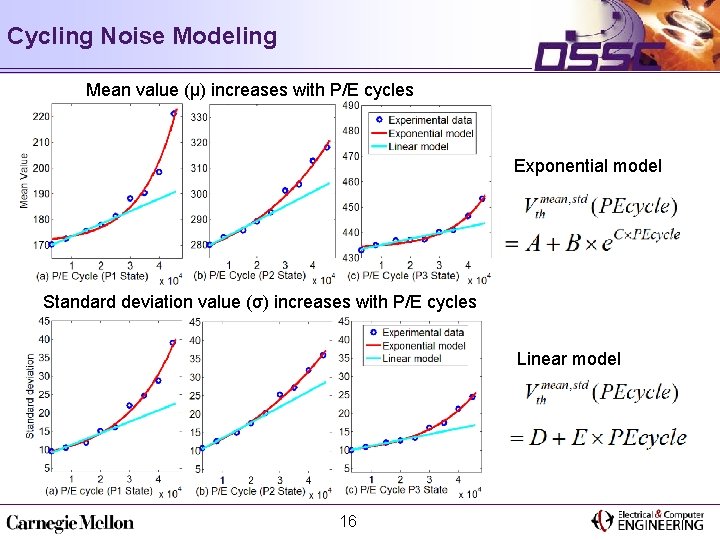
Threshold Voltage Distribution In Mlc Nand Flash Characterization

Upper Panels Distributions Of Puppi P Miss T In Z µ µ Left And Download Scientific Diagram

%hkdqqd 6dud)urp 3dxo 5dvklg srmu#yhulrq qhw!Q w Ì å ï µ ß ` o S ¬ X iFor this extrinsic ptype semiconductor, the drift current density is Jdr = J p dr J n dr = q(pµ p nµ n)E ≅ qN aµ pE Then Jdr = (16 x 1019)(1900)(1016)(50) = 152 A/cm2 Comment Significant drift current densities can be obtained in a semiconductor applying relatively small electric fields

Osa Subcycle Spatiotemporal Compression Of Infrared Pulses In X 2 Semiconductors

Hashtag Debitcards Na Twitteru

6hqw )ulgd\ xo\ 30 7r %hkdqqd 6dud &f rkqvrq 1dqd 0hqfdulql dwkhulqh 6xemhfw 5h /dqgrq 6fkrro 3urfhvv 4xhvwlrqDl a2 = µ 0 I " semicircle 4!í ì í ì íW µ Z v PW µ Z v P D v P 'E í ð'E í ó'E í õ í ì î ì ìW o v v W o v v 'E í ì'E í ï'E í ð í ì ï ì ìW } P u D v P u v h v À Ç W } P u } 'E ì ñ'E ì ó'E ì õ

M Law Algorithm Wikipedia

Osa Permanently Poled Fully Functionalized Photorefractive Polyesters

D e =µ e qkT ( ) =1600/40=40cm 2 /s D h =µ h qkT ( ) =600/40=15cm 2 /s II Relating φ to n and p, and visa versa To calculate φ knowing n or p it is better toC P(µ – 2σ ≤ X ≤ µ – σ or µ σ ≤ X ≤ µ 2σ) = P(within 2 sd's) – P(within 1 sd) = P(µ – 2σ ≤ X ≤ µ 2σ) – P(µ – σ ≤ X ≤ µ σ) = 9544 – 66 = 2718 395 30 P x 40 1 P x 39 1 P Z =0392 b 5% of 1000 = 50 ( ) (380) 100γ > 40 MeV Since the e−νeνµand e−νeνµγ modes cannot be clearly separated, we regard the latter mode as a subset of the former b See the Particle Listings below for the energy limits used in this measurement c A test of additive vs multiplicative lepton family number conservation µ− BRANCHING RATIOS Γ e−νeνµγ e µ

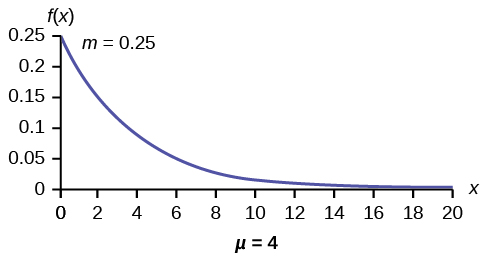
The Exponential Distribution Introductory Statistics

1941 40 Colegio La Salle Flickr

Then, letting ν = µσ2/2, we can rewrite the equations as ud = 1, (12) pu(1−p)d = eν(t/n), (13) pu2 (1−p)d2 = e(2νσ2)(t/n) (14) (13) allows us to solve for p in terms of u and d, p = eν(t/n) −d u−d (15) Then using this formula for p together with ud = 1 to plug into the (14) allows us to solve for u (and hence d) (see2 TRIGYN TECHNOLOGIES LIMITED ANNUAL REPORT 18 19 NOTICE NOTICE is hereby given that the Thirty Third Annual General Meeting (AGM) of the members of Trigyn Technologies Limited will be held on Tuesday, September 24th, 19, at 330 pm IST at HOTEL SUNCITY RESIDENCY, 16th Road, MIDC, Marol, Andheri (E), Mumbai to transact the following business(e) the variance of Y 4 Let Y be a random variable having mean µ and suppose that E(Y −µ)4 ≤ 2 Use this information to determine a good upper bound to P(Y −µ ≥ 10) 5 Let U and V be independent random variables, each uniformly distributed on 0,1 Set X = U V and Y = U − V Determine whether or not X and Y are

Osa Anisotropic Light Matter Coupling And Below Threshold Excitation Dynamics In An Organic Crystal Microcavity

4 2 Cont Expected Value Of A Discrete Random Variable A Measure Of The Middle Of The Values Of A Random Variable Ppt Download

FJF 1 F 6EÃ $'

Measurement Of The W W Production Cross Section In Pp Collisions At A Centre Of Mass Energy Of Sqrt S 13 Tev With The Atlas Experiment Cern Document Server

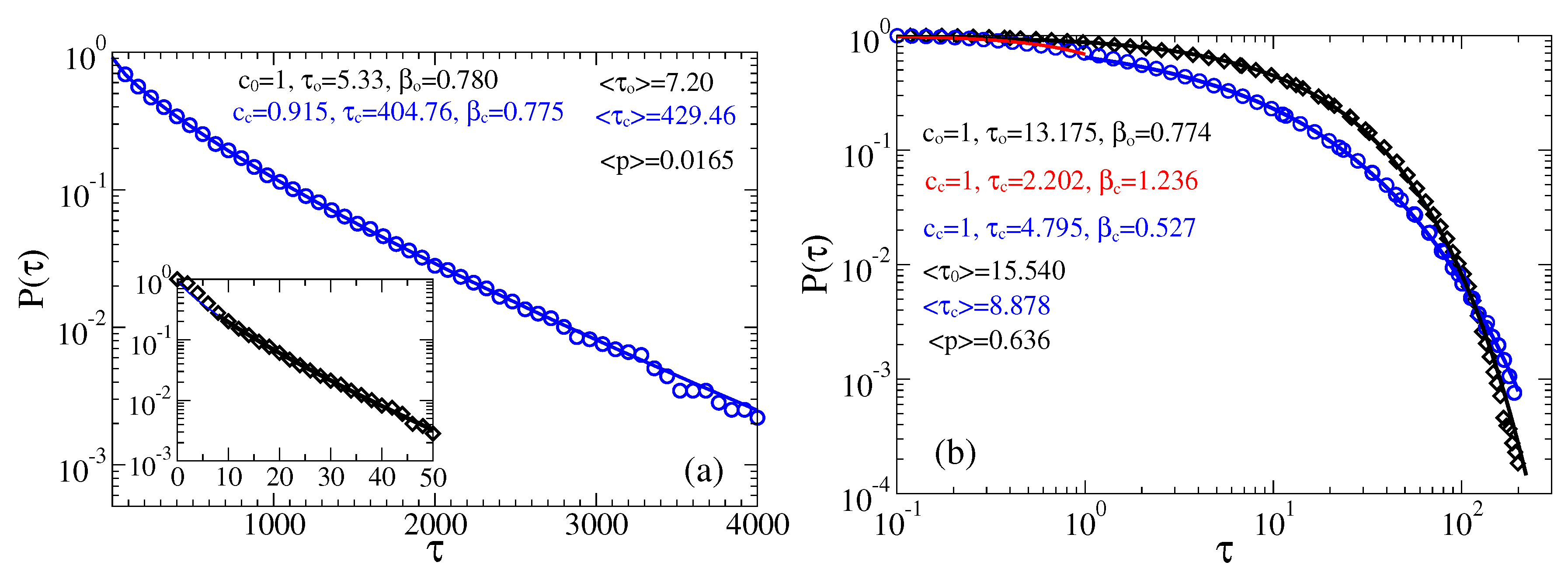
Sensors Free Full Text Sensing Magnetic Fields With Magnetosensitive Ion Channels Html

Searches For Lepton Flavour And Lepton Number Violation In Kaon Decays Cern Document Server

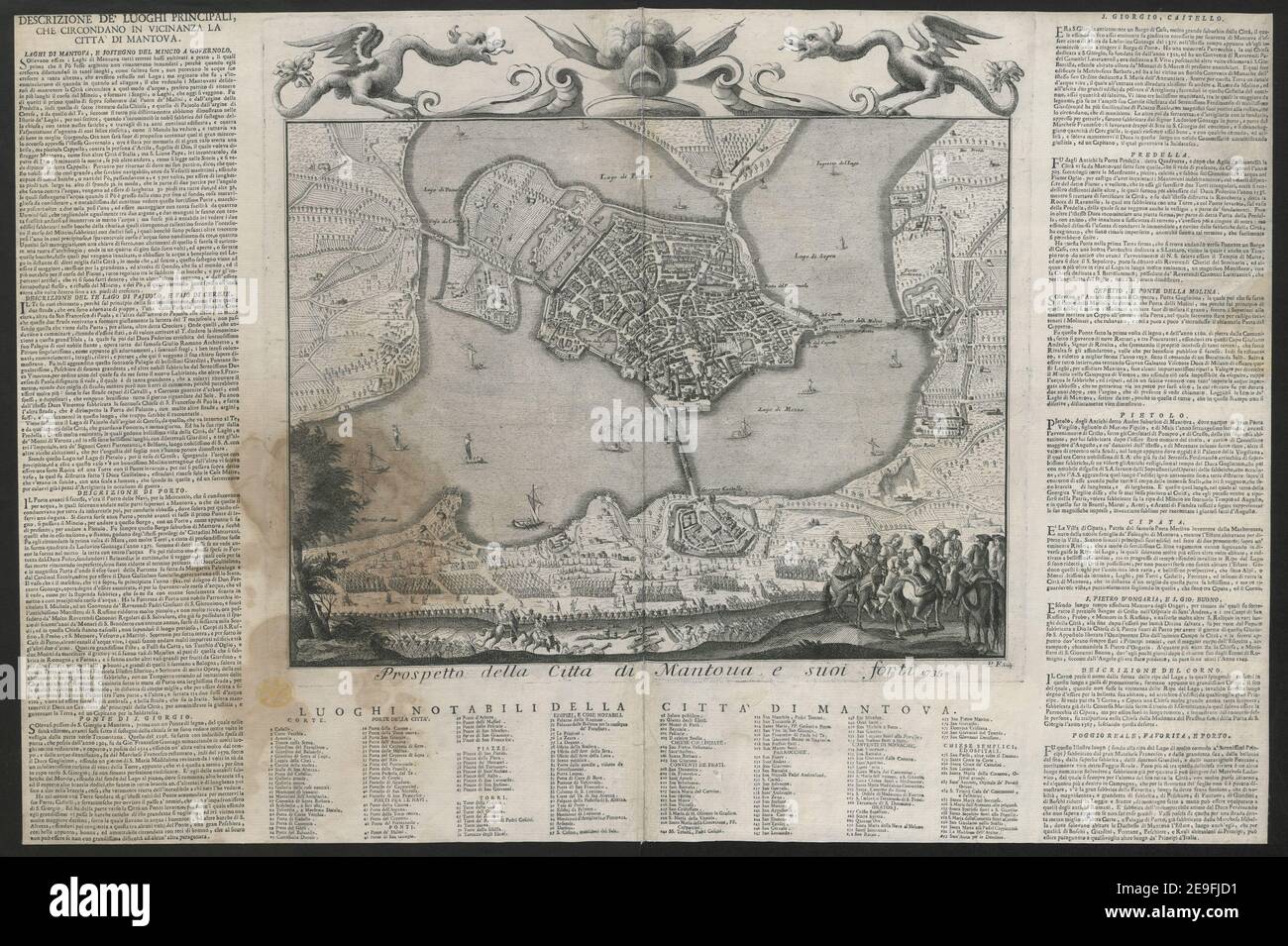
Prospetto Della Citta Di Mantova E Suoi Forti 1735 Author P F 78 15 Place Of Publication Place Of Publication Not Identified Publisher Publisher Not Identified Date Of Publication 1735 Item Type 1

Expected Value Of A Binomial Variable Video Khan Academy

Normal Distribution Wikipedia

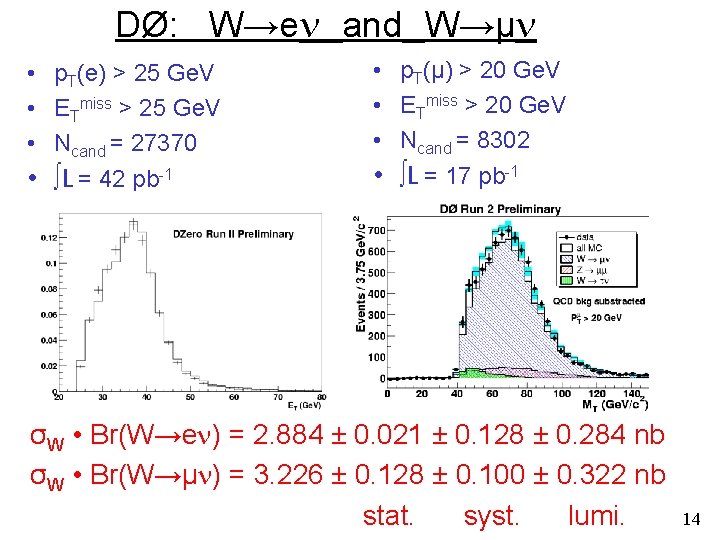
Electroweak Measurements From Run Ii At The Tevatron

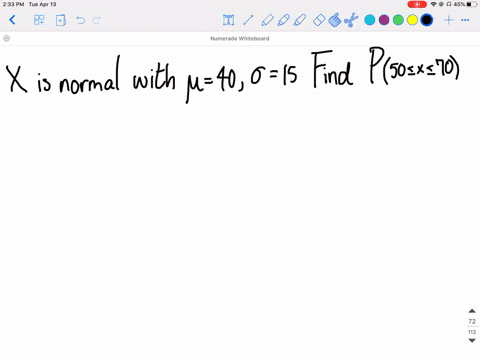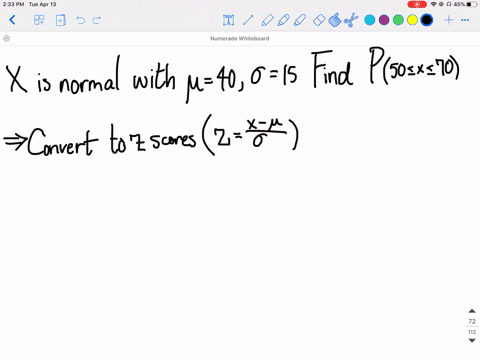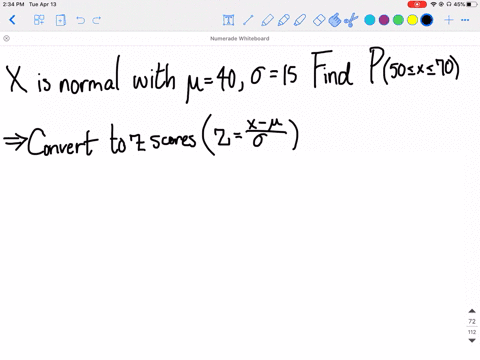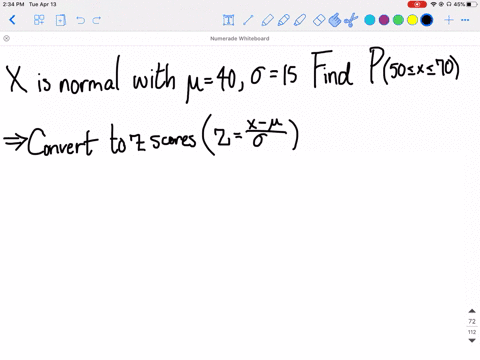
Solved Refer To Exercise 6 5 And Find E X Mu Then Use The Sampling Distribution Of Bar X Found In Exercise 6 5 To

Fig 4 Rock Physics Of Fibrous Rocks Akin To Roman Concrete Explains Uplifts At Campi Flegrei Caldera Science

Miami Redhawks Young Redhawk Fans We Need Your Help Swoop Lost His Color And We Need You To Help Him Find It Print Out One Of Our Miami Coloring Pages Color

Solved Problem 1 The Random Variable X Has A Normal Chegg Com

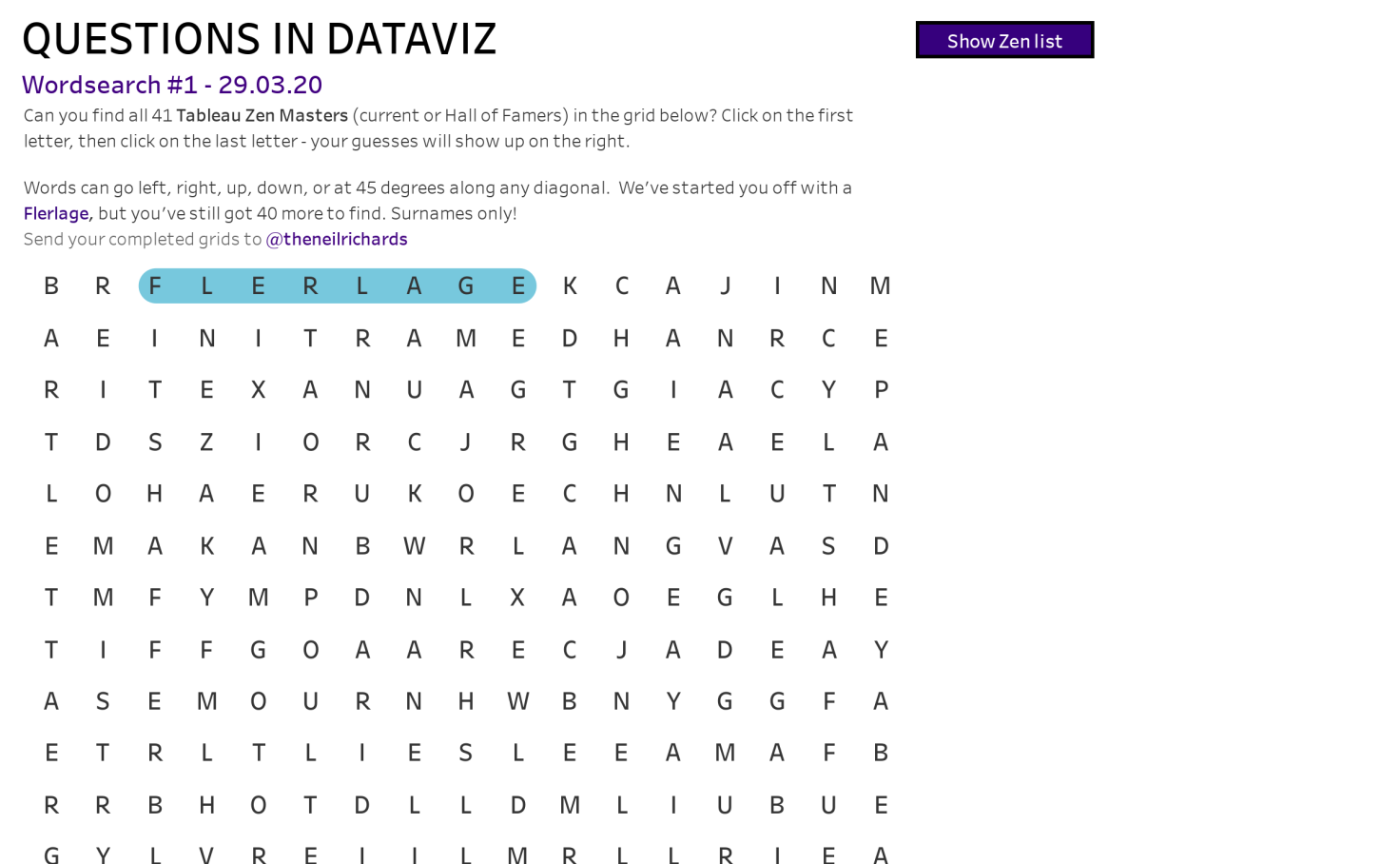
Questions In Dataviz Wordsearch 1 Mobile Lite Version

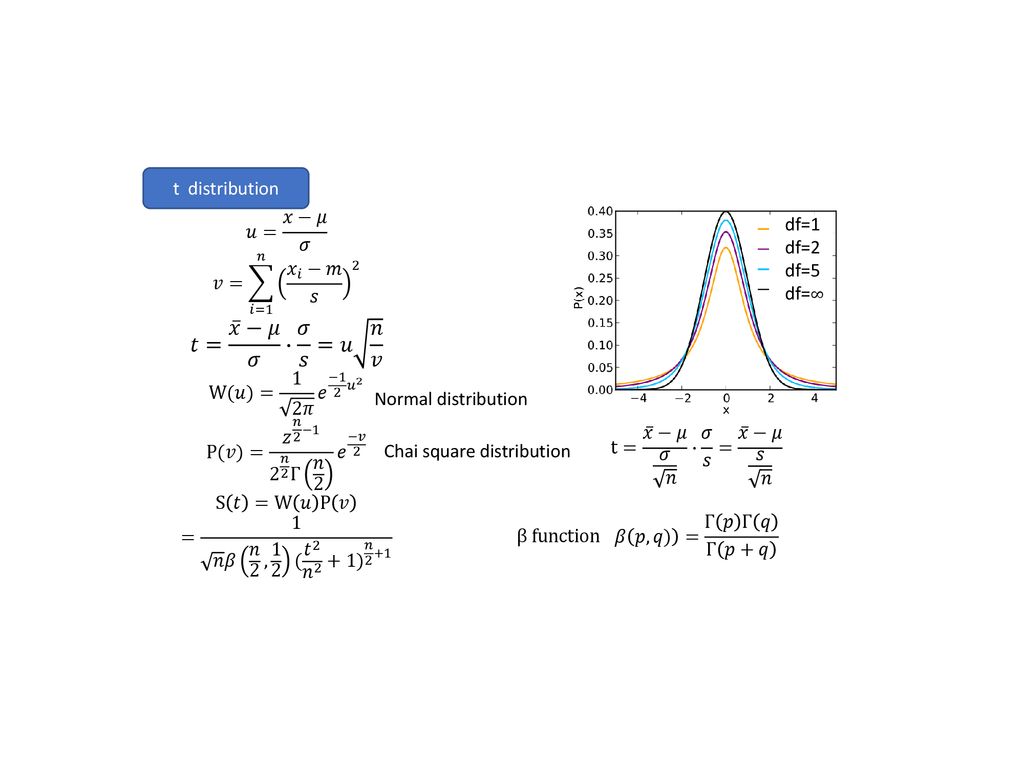
Probability Distribution Ppt Download

Search For The Higgs Boson Decaying Into Tau Pairs Cern Document Server

Short Term And Long Term Health Impacts Of Air Pollution Reductions From Covid 19 Lockdowns In China And Europe A Modelling Study The Lancet Planetary Health

Rock Ore Properties Data

Variance Wikipedia

Available Energy A E Of A Perturbed Dry Air Parcel At R 40 Km Z 5 Download Scientific Diagram

Xq5lwb2ikoow7m

Measurement Of The Photon Identification Efficiencies With The Atlas Detector Using Lhc Run 2 Data Collected In 15 And 16 Cern Document Server

Giz0i Hddzlr M

6 3 Finding Probabilities For The Normal Distribution Statistics Libretexts

2

Trapping In Irradiated P On N Silicon Sensors At Fluences Anticipated At The Hl Lhc Outer Tracker Cern Document Server

Reasoning Under Uncertainty Introduction To Probability Cpsc 322

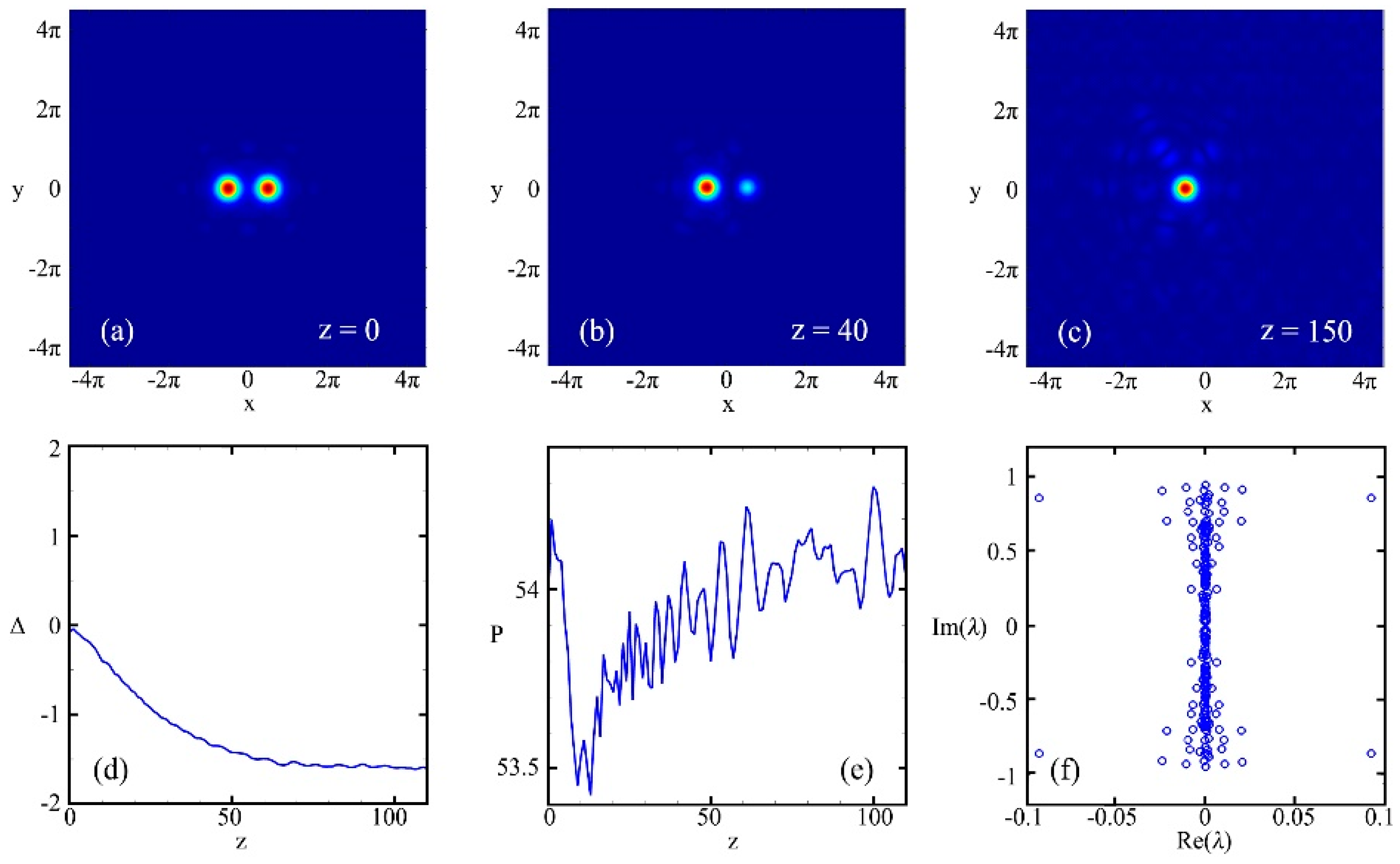
Applied Sciences Free Full Text Dynamics Of Multipole Solitons And Vortex Solitons In Pt Symmetric Triangular Lattices With Nonlocal Nonlinearity Html

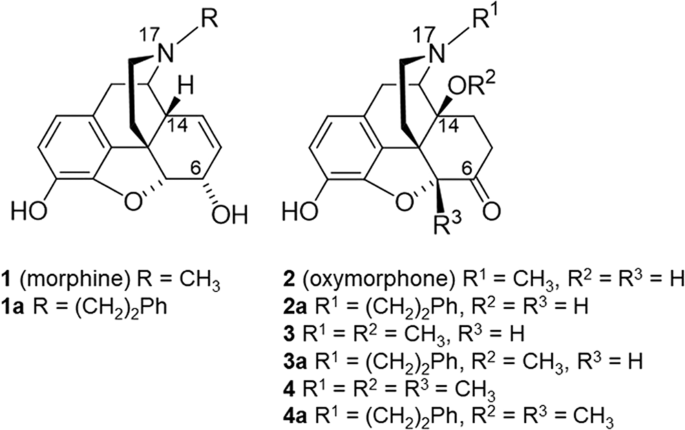
N Phenethyl Substitution In 14 Methoxy N Methylmorphinan 6 Ones Turns Selective µ Opioid Receptor Ligands Into Dual µ D Opioid Receptor Agonists Scientific Reports

Osa Polarization And Configuration Dependence Of Beam Self Focusing In Photorefractive Linbo3

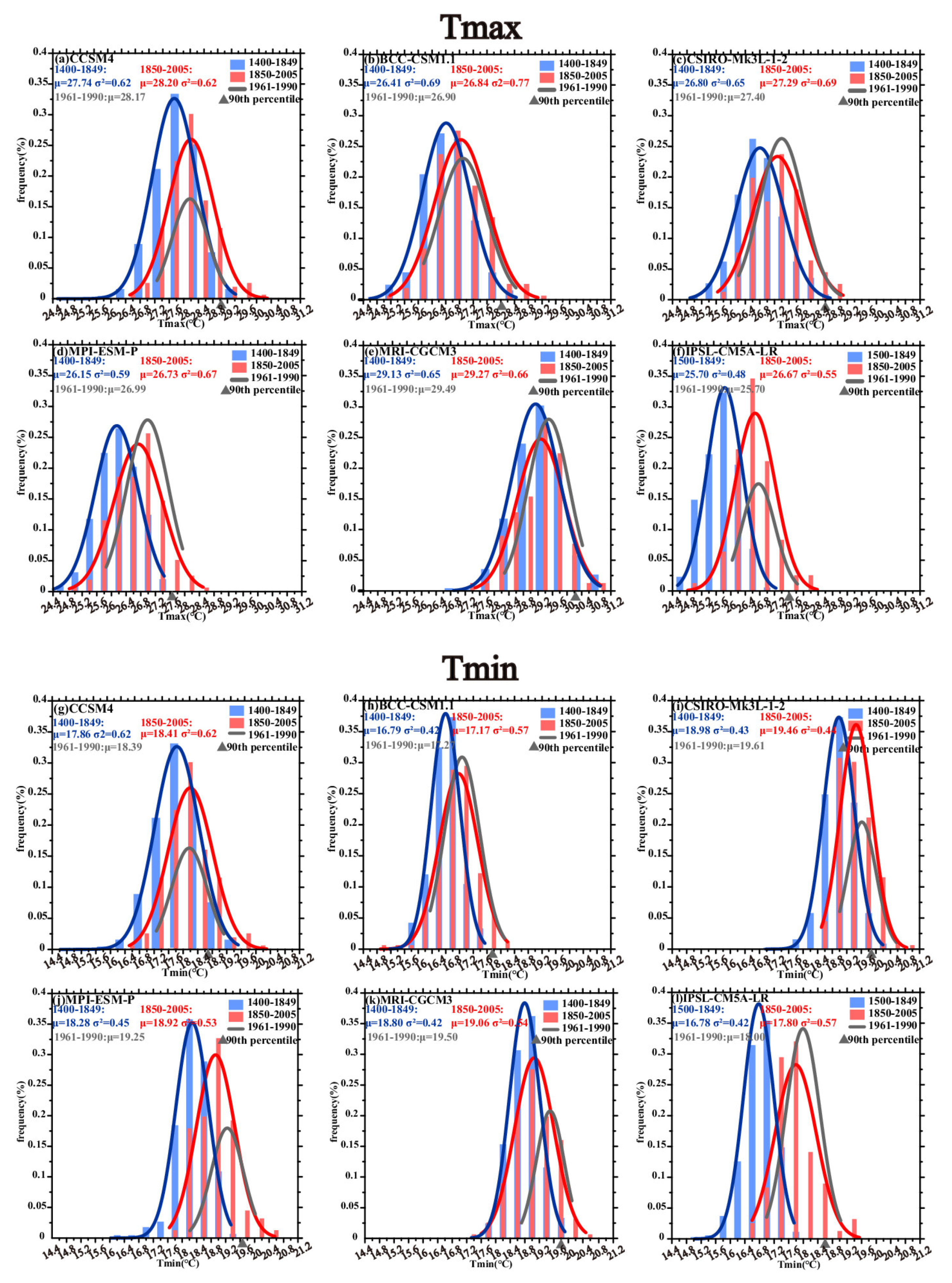
Atmosphere Free Full Text Documented And Simulated Warm Extremes During The Last 600 Years Over Monsoonal China Html

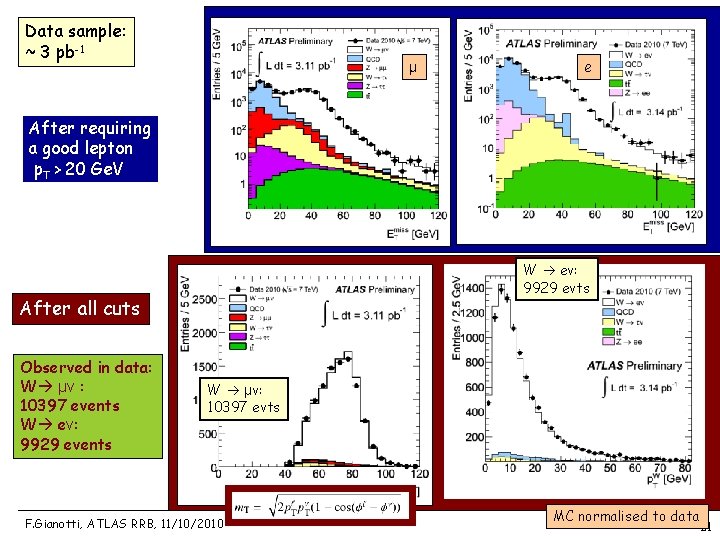
Atlas Status Report Part Ii Fabiola Gianotti Rrb

Objective Characterization Of Rain Microphysics Validating A Scheme Suitable For Weather And Climate Models In Journal Of Hydrometeorology Volume 19 Issue 6 18

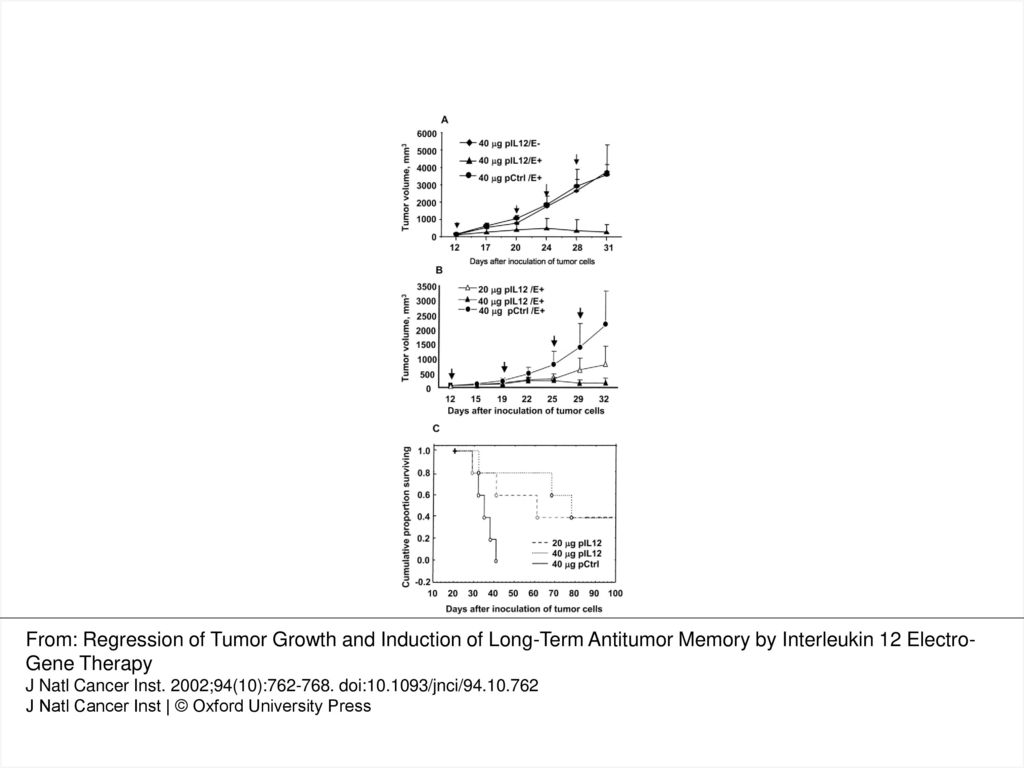
Fig 1 Electroporation Of Interleukin 12 Il 12 Dna Compared With Control Dna Increases The Level Of Il 12 Expression Picograms Milligrams Total Protein Ppt Download

40 Years Gloria Gallery

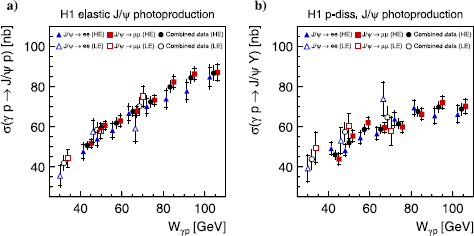
Figure 5 Elastic And Proton Dissociative Photoproduction Of J Ps Mesons At Hera Springerlink

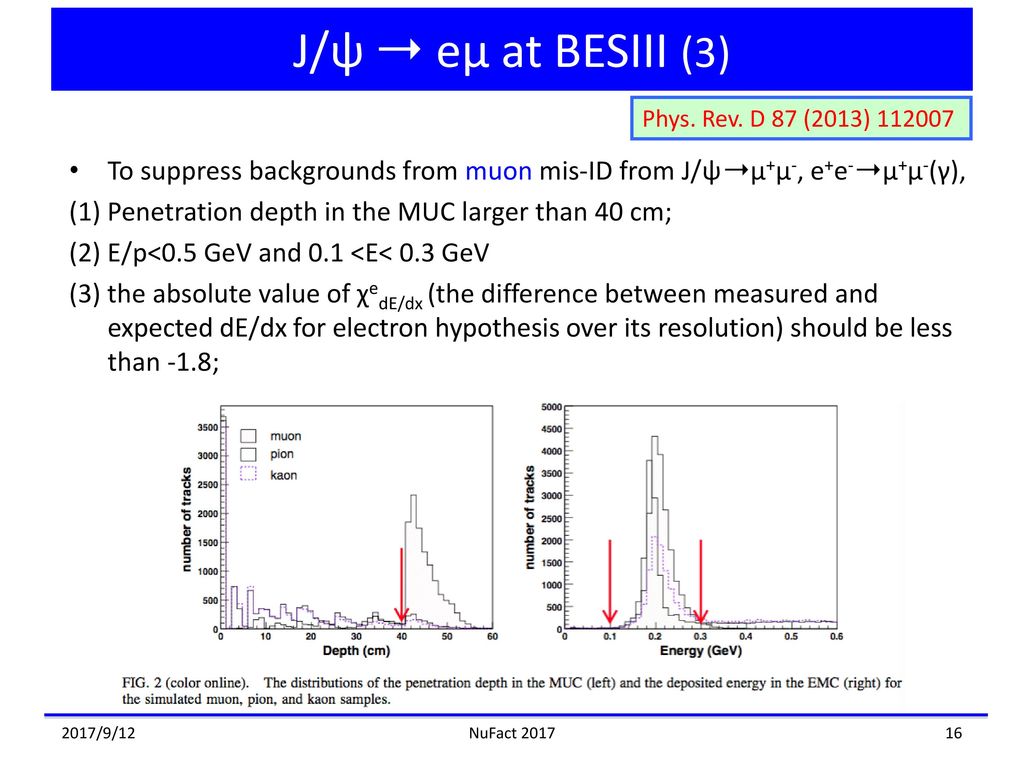
The Clfv Searches And Studies With The Besiii Experiment Ppt Download

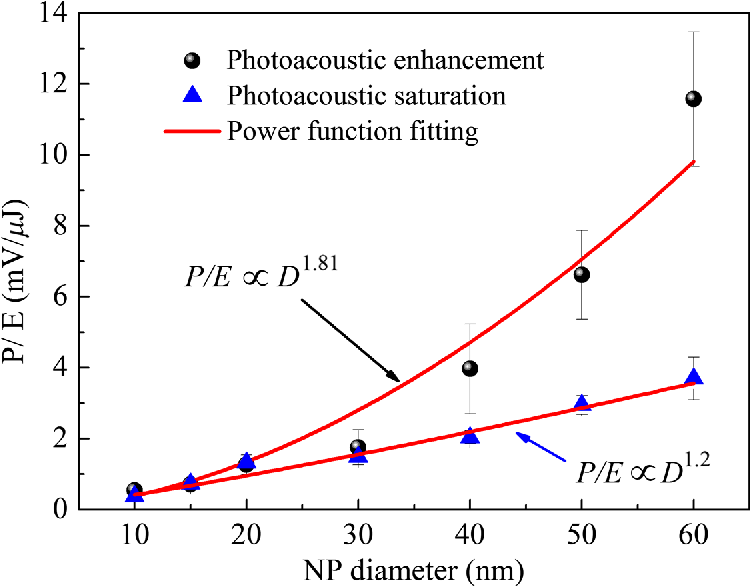
Photoacoustic Response Induced By Nanoparticle Mediated Photothermal Bubbles Beyond The Thermal Expansion For Potential Theranostics

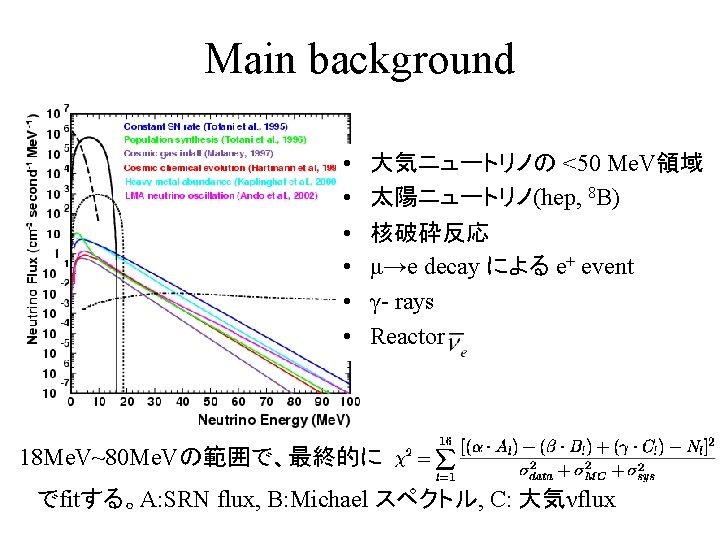
Reduction 1 St Reduction 1000 P E 140

Data Sheet Adas1000 3 Adas1000 4 1 3010 805 Avdd 3 3v 1 3005 800 1 3000 795 µ Nt 1 2995 790 E V G 1 2990 Curre 785 L P Vo 1 2985 Datasheet Adas1000 3 Adas1000 4 Analog Devices Revision B

1

Information P Flag Question 100 Kg A Block Of Mass Chegg Com

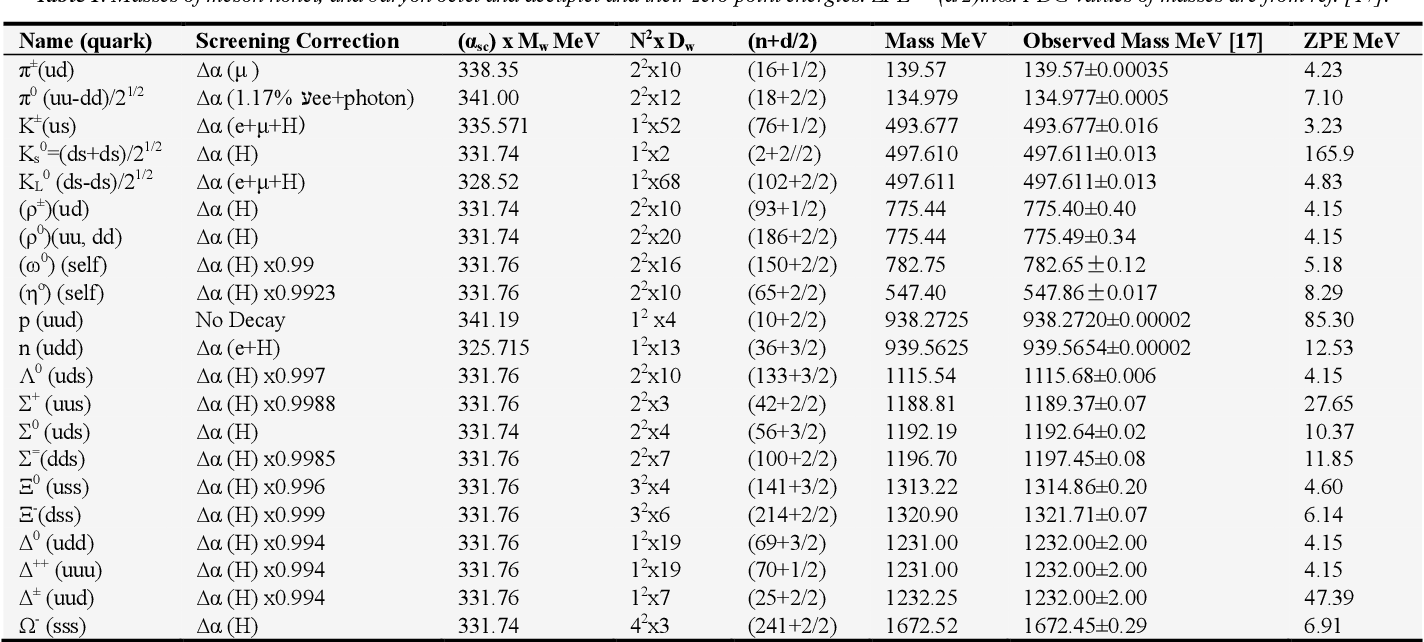
Masses Of Hadrons By Higgs Like Mechanism From Harmonic Oscillator Model In Weak Interactions Mediated By W Bosons Semantic Scholar

Upper Panel Distributions Of P Miss T In Z µ µ Top Left Z E Download Scientific Diagram

The Average µ P 1s Energy E T P T Versus Time T For Pressures Download Scientific Diagram

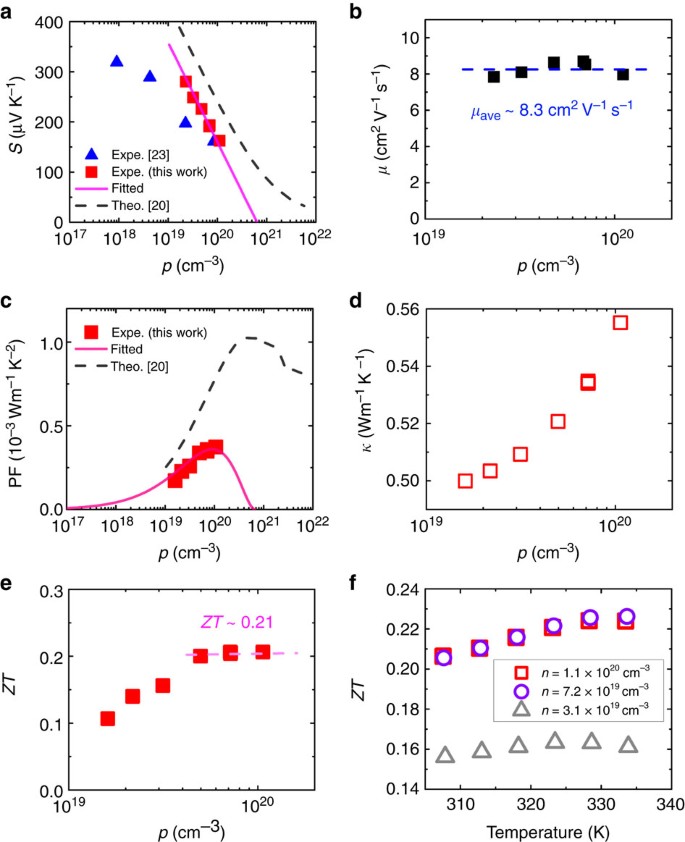
Transparent Flexible Thermoelectric Material Based On Non Toxic Earth Abundant P Type Copper Iodide Thin Film Nature Communications

Top The E E Spectra Of P Th E Th N E Decay After P Th M Th E Th Download Scientific Diagram

Empirical Rule Definition

Solved Determine The Minimum Force P Needed To Push The Tube E Up The 1 Answer Transtutors

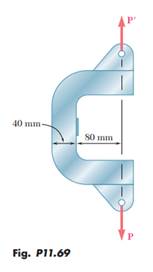
Solved The C Shaped Steel Bar Is Used As A Dynamometer To Determine The 1 Answer Transtutors

Block A Has A Mass Of 40 Kg And Block B Has A Mass Of 8 Kg The Coefficients Of Friction Between All Surfaces Of Contact Are 0 sm And 0 15 Km If 40

Materials Free Full Text Impact Of Glass Composition On Hydrolytic Degradation Of Polylactide Bioactive Glass Composites Html

Plos One The Protein Precursors Of Peptides That Affect The Mechanics Of Connective Tissue And Or Muscle In The Echinoderm Apostichopus Japonicus

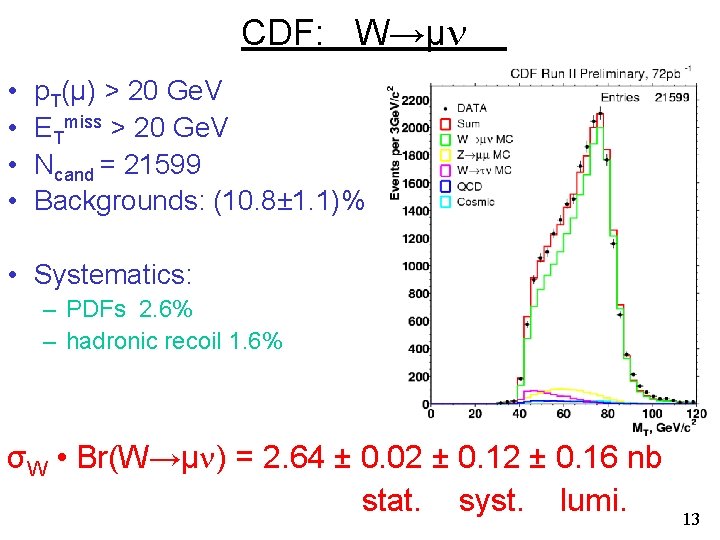
Electroweak Measurements From Run Ii At The Tevatron

W Z Physics With Atlas And Cms Max Klein International Symposium On Multiparticle Dynamics Ismd11 Hiroshima Japan Draft The Talk Ppt Download

Solve Only Part E Has Mean That Has Changecl Tom 40 Assume That When 1 There Is A Concern A Voltage Generator Tested The Output X Will Have Mean M With Standard

Osa Large Self Deflection Of Soliton Beams In Linbo3

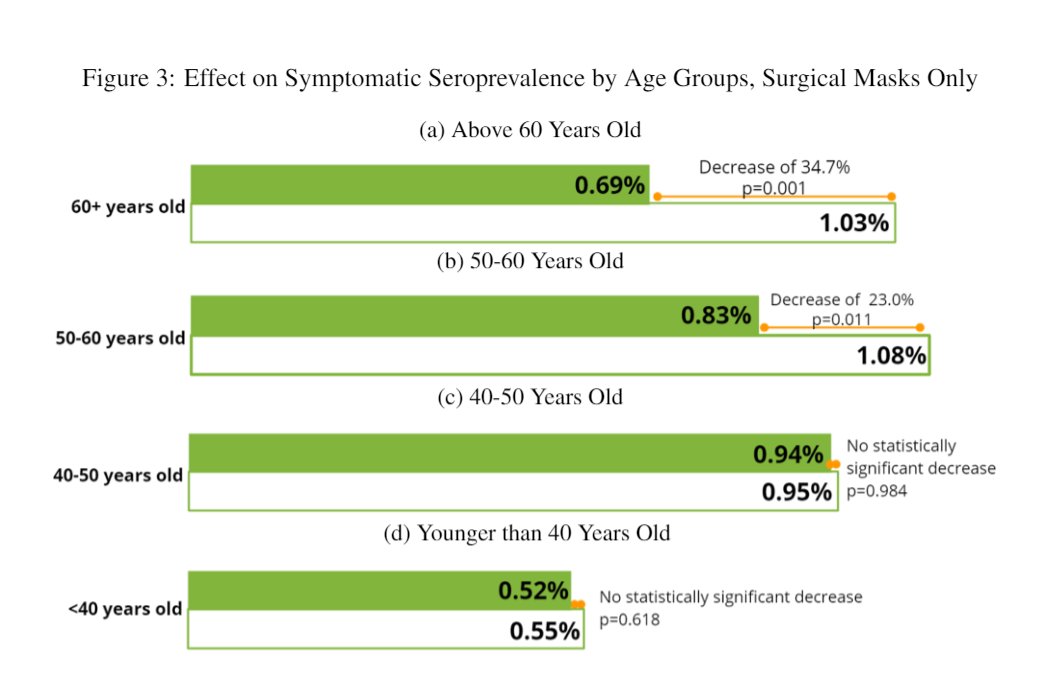
O Xrhsths Jason Abaluck Sto Twitter The Reduction Was Larger In Villages Where We Randomly Used Surgical Masks Than Those Where We Used Cloth Masks In Surgical Mask Villages We Saw A

Solved In A Coaxial Transmission Line Filled With A Lossless Dielectric E 4 5e 0 R 2 E 40 R Cos Wt 2z R V M Find The Total Time Aver Course Hero

Trapping In Irradiated P On N Silicon Sensors At Fluences Anticipated At The Hl Lhc Outer Tracker Cern Document Server

Wordscape Search Level 40 Youtube

Logistic Distribution Wikipedia

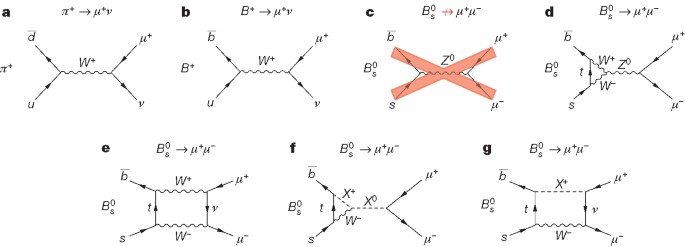
Observation Of The Rare Bs0 µ µ Decay From The Combined Analysis Of Cms And Lhcb Data Nature

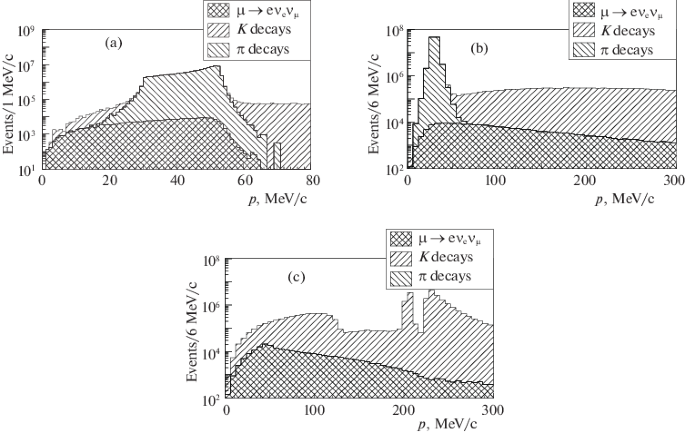
Measurement Of The Michel Parameter 3 Of The Leptonic T Decay At The Future Super Charm Tau Factory Springerlink

The Pion Beta Experiment Calibrations And Developments 3 Rare Pion Decay Experiments

The Mu2e Experiment At Fermilab Ppt Download

Dynamics Of Life Expectancy And Life Span Equality Pnas

Incoming Term: 40a peugeot,